Reliability

2. 展開公式

1章では、各辺の正常/故障のパターンをすべて調べることによってネットワーク信頼度Rel(G)を計算した。しかし、このやりかたでは、辺数をmとして、2^m通りのパターンを調べる必要があり、もう少し規模の大きいネットワークに対して計算しようとするとかなりの労力を必要とすることになる。もう少し頭の良い計算法はないだろうか？

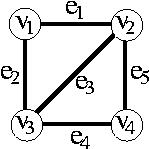
ネットワークのある特定の1辺に着目してみよう。どの辺でもよいが、例えば、e₁に着目してみる。

この辺、e₁は、正常に機能するか、もしくは、故障しているか、どちらかである。確率pで前者、確率(1－p)で後者が起こることになる。

このとき、

辺e₁が正常に機能しているという条件下で、ネットワークが正常に機能する確率をP₁、
辺e₁が故障しているという条件下で、ネットワークが正常に機能する確率をP₂

とすると、

Rel(G) = p×P₁＋(1-p)×P₂

と計算できるはずである。そこで、このP₁とP₂について考えてみよう。

まず、P₂の方を考えてみる。これは、辺e₁が故障しているという条件下でネットワークが機能する確率である。このとき、辺e₁は故障しているのだから、この辺は取り除いてしまい、次の右側のようなネットワークを考えても同じである。

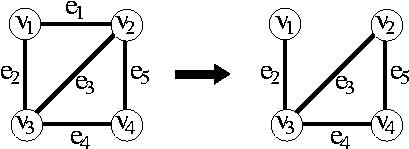
このe₁を取り除いたネットワークをG₂と名付ければ、 P₂＝Rel(G₂) と書くことができることになる。

それでは、P₁の方はどうだろうか。こちらは、辺e₁が正常に機能しているという条件下でネットワークが機能する確率である。つまり、辺e₁は必ずその両端点v₁とv₂を(故障することなく)つないでいる。ということは、下の図のように、e₁を縮め、v₁とv₂を一つのノードにしてしまったのと同じことになるはずである。

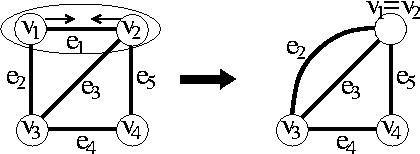
つまり、図の右側のネットワークをG₁と書けば、 P₁＝Rel(G₁) となるわけである。

以上をまとめてみると、Rel(G)＝p・Rel(G₁)＋(1－p)・Rel(G₂)、つまり、

のような公式で計算することができるということである。右辺に現れるネットワークにも同じ公式を次々と適用していくことによって、例えば次のように計算できる。

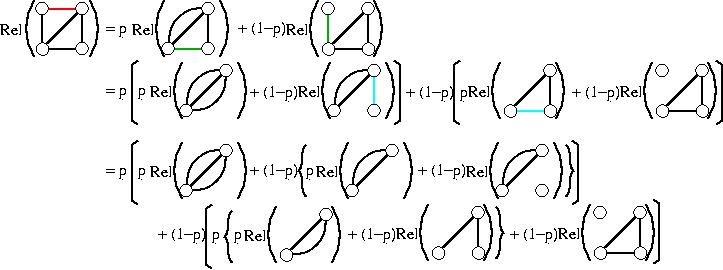
(まず赤い辺に公式を適用し、次に緑の2辺に適用し、次に水色の2辺に適用している。)

ここまで計算すると、

すでに非連結になっているネットワークに関しては、ネットワーク信頼度は0である。
k辺が並列に並ぶネットワークの場合には、すべての辺が故障するとき以外は連結になるので、Rel＝1-(1-p)^kとなる。
k辺が直列に並ぶネットワークの場合には、すべての辺が正常であるときにのみ連結になるので、Rel＝p^kとなる。

という簡単な計算を用いれば、

Rel(G)＝p[p(1-(1-p)³) + (1-p){p(1-(1-p)²)+(1-p)・0]
+(1-p)[p{p(1-(1-p)²)+(1-p)p²}+(1-p)・0]
＝4p⁵－11p⁴＋8p³

と計算することができる。

（注）
この展開公式においては、どの辺に注目して展開しても同じ結果になる。

<1章へ | 目次 | 3章へ>