1. ネットワークの信頼度を計算しよう

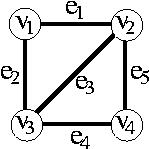
下図のようなネットワークGがあったとしよう。

このネットワークは、コンピュータやサーバを結ぶ回線のネットワークと思ってもよいし、または、道路のネットワークと思ってもよい。

現在、このネットワークでは、4つのノードが5つの辺で結ばれていて、 どの2つのノードに対しても、うまく経路を選べばその2つのノードをつなくことができるようになっている。 例えば、v₁とv₄であれば、 e₁−e₅やe₂−e₃−e₅などの経路を辿ってつなぐことができている。 つまり、コンピュータのネットワークであれば、どの2つの間でも通信を行なうことができるし、道路ネットワークであれば、どの2点間も行き来出来る状態になっている、ということであり、ネットワークが正常に機能している状態であるということができる。

しかし、今仮に、2つの辺e₁とe₂が(回線が切れた、道路工事などの理由で)故障してしまったとしよう。

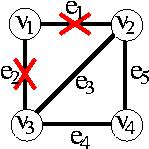
すると、例えば、v₁とv₃をつなぐ経路はなくなってしまい、 通信(もしくは行き来)ができなくなってしまう。 つまり、ネットワークとして正常に機能できないことになってしまう。

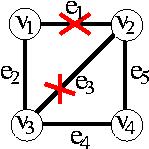
一方、同じ2つの辺の故障でも、故障した辺がe₁とe₃であれば、 どの2ノード間でも通信できることが確認できるだろう。

それでは、各辺の故障確率が分かっているとして、このネットワークが正常に機能する状態である確率がどのくらいになるのか、計算してみよう。

簡単のため、各辺は同じ確率(1−p)で故障するものとしよう。 つまり、各辺は確率pで正常に機能し、確率(1−p)で故障する。 5辺の正常/故障のパターンをすべて列挙してみると、下のようになる。 (「○」は正常、「×」は故障を表している。)

e1 e2 e3 e4 e5 起こる確率 ネットワークの状態 ○ ○ ○ ○ ○ p5 正常(連結) ○ ○ ○ ○ × p4(1−p) 正常(連結) ○ ○ ○ × ○ p4(1−p) 正常(連結) ○ ○ × ○ ○ p4(1−p) 正常(連結) ○ × ○ ○ ○ p4(1−p) 正常(連結) × ○ ○ ○ ○ p4(1−p) 正常(連結) ○ ○ ○ × × p3(1−p)2 故障(非連結) ○ ○ × ○ × p3(1−p)2 正常(連結) ○ ○ × × ○ p3(1−p)2 正常(連結) ○ × ○ ○ × p3(1−p)2 正常(連結) ○ × ○ × ○ p3(1−p)2 正常(連結) ○ × × ○ ○ p3(1−p)2 正常(連結) × ○ ○ ○ × p3(1−p)2 正常(連結) × ○ ○ × ○ p3(1−p)2 正常(連結) × ○ × ○ ○ p3(1−p)2 正常(連結) × × ○ ○ ○ p3(1−p)2 故障(非連結)

e1 e2 e3 e4 e5 起こる確率 ネットワークの状態 ○ ○ × × × p2(1−p)3 故障(非連結) ○ × ○ × × p2(1−p)3 故障(非連結) ○ × × ○ × p2(1−p)3 故障(非連結) ○ × × × ○ p2(1−p)3 故障(非連結) × ○ ○ × × p2(1−p)3 故障(非連結) × ○ × ○ × p2(1−p)3 故障(非連結) × ○ × × ○ p2(1−p)3 故障(非連結) × × ○ ○ × p2(1−p)3 故障(非連結) × × ○ × ○ p2(1−p)3 故障(非連結) × × × ○ ○ p2(1−p)3 故障(非連結) ○ × × × × p(1−p)4 故障(非連結) × ○ × × × p(1−p)4 故障(非連結) × × ○ × × p(1−p)4 故障(非連結) × × × ○ × p(1−p)4 故障(非連結) × × × × ○ p(1−p)4 故障(非連結) × × × × × (1−p)5 故障(非連結)

ここで、ネットワークが連結になるパターンの確率をすべて足し合わせれば、 ネットワークが正常に機能する確率Rel(G)を計算することができる。つまり、

Rel(G)＝ 1×p⁵ ＋ 5×p⁴(1−p) ＋ 8×p³(1−p)² ＋ 0×p²(1−p)³ ＋ 0×p(1−p)⁴ ＋ 0×(1−p)⁵
＝ 4p⁵ − 11p⁴ ＋ 8p³

が求める確率ということになる。 例えば、p＝0.9の場合には、この確率は約0.977となる。

この、ネットワークが正常に機能する確率、つまり、 ネットワークが連結になる確率は、ネットワーク信頼度(network reliability)と呼ばれている。 これは、このネットワークが、各辺の故障に関してどの程度頑健であるかを見る尺度である。

上では簡単のためにすべての辺の故障確率をpにしているが、 一般にはそれぞれの故障確率は異なる値を与えることができる。 上でやったようにすべての辺の故障確率をpとすると、ネットワーク信頼度はpの多項式になる。 この多項式は、信頼度多項式(reliability polynomial)と呼ばれている。

(注)
ここでは、任意の2ノード間で通信が可能であることをネットワークが正常であることとしたが、 この場合のネットワーク信頼度は正確には、「全端点信頼度」(all-terminal reliability) と呼ばれるものである。 特定の2ノード間で通信ができればよい(2-terminal reliability)、とか、 特定のkノード間で通信ができればよい(k-terminal reliability)、 などのバリエーションもある。 また、各辺における通信に方向が定まっているようなバリエーションもある。