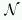6.ネットワーク信頼度を見積もろう

A(G)≦Rel(G)≦B(G)

を満たすようなA(G)とB(G)をうまく計算することによってRel(G)の大体の値を見積もろう、ということである。 ここでは、各辺の故障確率はすべてpとして、信頼度多項式について考えることとしよう。

まず、信頼度多項式を別の形で書き直してみる。 1章での計算を思い出してみると、信頼度多項式を計算するためには、 ネットワークを連結にすることができる故障パターンを全部調べて、 その故障パターンが起きる確率を足し合わせればRel(G)を得ることができた。 ここで、 ネットワークは連結になるような、m本の辺中i本の辺が正常である場合の故障パターンの個数をN_iとすると、

Rel(G)=N₀p⁰(1ーp)^m＋N₁p¹(1ーp)^m-1＋N₂p²(1ーp)^m-2＋…＋N_mp^m(1ーp)⁰

のように書けることが分かる。 ここで、N_iは、ネットワークGの辺の集合の部分集合で、すべてのノードをつなぐことができるものの全体、すなわち、

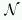＝{X⊆E：Xはすべてのノードをつなぐ}

を考え、その中でサイズがiのものの個数をそれぞれ数えた、ということである。

別の見方をすると、ネットワークは連結になるような、i本の辺が故障した場合の故障パターンの個数をF_iとして、

Rel(G)=F₀p^m(1ーp)⁰＋F₁p^m-1(1ーp)¹＋F₂p^m-2(1ーp)²＋…＋F_mp⁰(1ーp)^m

のように書くこともできる。(N_i＋F_i＝_mC_iになる。) こちらは、 ネットワークGの辺の集合の部分集合で、それらを取り除いてもすべてのノードをつなぐことができるものの全体、すなわち、

＝{X⊆E：EからXを取り除いた残りの辺がすべてのノードをつなぐ}

を考え、その中でサイズがiのものの個数をそれぞれ数えたものをF_iとした、ということである。

この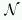やの(それぞれのサイズの)要素の個数が分かればRel(G)を計算することができ、それをやったのが1章の計算例だったのであるが、これらを実際に計算することをしないで、上限・下限を求めたいのである。

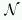やはEという集合の部分集合からなる集合になっている。 このようなものを、(Eを台集合とする)集合族という。

一つの手がかりとして、は部分集合に閉じている、という性質がある。 つまり、Xという部分集合がに含まれる場合、Xの部分集合もに含まれる ということである。(故障する辺が少なくなるので当然そうなる。) このように部分集合に閉じている集合族は、「単体的複体」と呼ばれている。 (この名称は、位相幾何学という分野でよく使われる単体的複体という幾何学的な概念と密接な関係があることから用いられる専門用語である。「独立集合族」やその他の名前で呼ばれることもある。)

例えば、1章で例に使ったネットワーク

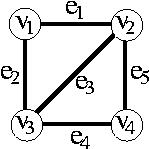
の場合、

＝ { φ, {e₁}, {e₂}, {e₃}, {e₄}, {e₅}, {e₁,e₃}, {e₁, e₄}, {e₁,e₅}, {e₂,e₃}, {e₂, e₄}, {e₂,e₅}, {e₃,e₄}, {e₃,e₅} } となっている。例えば、{e₁,e₃}の部分集合である{e₁},{e₃},φはすべて要素になっていることが確認できる。

単体的複体に関しては、次の有名な定理が知られている。

スペルナーの定理 台集合のサイズがmである単体的複体において、サイズがiの要素の個数をFiとすると、 Fi-1 ≧ (i／(m−i＋1))・Fi が成り立つ。

(証明は比較的簡単なので、各自考えてみよう。 → 証明を見る)

これを用いると、次のようにRel(G)の上限・下限を与えることができる。

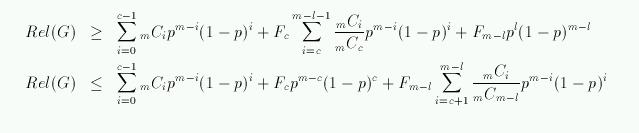
ただし、ここでは、次のようなことを使っている。

• ネットワークを故障させるのに最小限取り除く必要のある辺数をcとする。 c未満の辺の故障ではネットワークは故障しないので、 i＜cの場合はF_i＝_mC_iとなる。
• ネットワークを故障させないで取り除ける最大限の辺数をlとする。 lより大きい本数の辺の故障は必ずネットワークを故障させるので、 i＞lの場合はF_i＝0となる。
• lは「辺の数−頂点数＋1」。 F_lはグラフの全域木の個数と一致し、効率的に計算する方法が知られている。
• cはグラフの最小カットの辺数で、これは効率的に計算することができる。また、 F_cは最小カットの個数で、これも効率的に計算する方法が知られている。
• それ以外の場合は、スペルナーの定理の不等式を F_i ≦ ((m−i＋1)／i)・F_i-1 として、F_cから順番にF_c+1、F_c+2、…と評価していくと上限を得ることができる。
  逆に、 F_i-1 ≧ (i／(m−i＋1))・F_i として、F_lから順番にF_l-1、F_l-2、…と評価していくと下限が得られる。
  (このように順番に評価していくと、分数をたくさん掛け合わせる形になるが、それを上の式では二項係数を使ってきれいな形にまとめている。)

(上の式は一見かなり複雑であるが、コンピュータを使って計算することを考えると計算は楽。)

これはスペルナーの定理という比較的簡単に考察できる定理を使って得られる上下限であるが、 これをもっと精密化した「クルスカル・カトナの定理」を用いた「クルスカル・カトナ限界」、 さらに、がただの単体的複体ではなく、コーエン・マコーレーと呼ばれる性質を持つ単体的複体であるという性質を用い、マコーレーの定理を用いて得られる「スタンレー限界」、また、その改良など、種々の研究がなされている。 (は、もっと強い「シェラブル」という性質も持っている。)

これらの上下限を与える元になっているスペルナーの定理、クルスカル・カトナの定理やコーエン・マコーレー性は、ネットワーク信頼度などの議論とは全く別個に、 離散数学や組合せ論という分野で純粋な数学的対象として研究されてきたものであり、また、 現在も様々な研究が進められている。 極値集合論の他、トポロジー的・幾何学的組合せ論、可換代数と組合せ論、などの分野の研究が深く関連している。

次の7章で、コーエン・マコーレー性を用いたスタンレー限界はどんな感じで議論されるのか、ほんの触りだけ紹介してみる。