4.ネットワーク信頼度とタット多項式
2章の展開公式では、注目した辺に関して、2種類の操作が登場した。
- 辺を縮め、両端のノードを一つにまとめる
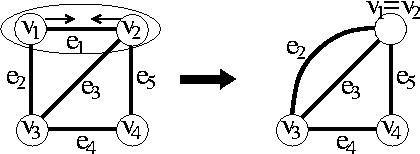
- 辺をネットワークから取り除く
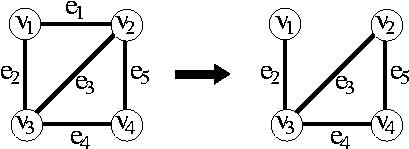
これまで、ネットワークをノードとそれらを結ぶ辺で記述してきたが、
このようなものは「グラフ理論」の世界では「グラフ」(graph)と呼ばれている。
(この文章中でネットワークの名前にGとかG1という名前をつけているのは、実はこの「グラフ」の頭文字のGを念頭においているのである。)
そして、上の2種類の操作はそれぞれ、辺の「縮約」(contraction)、辺の「除去」(deletion)という名前で知られている。
グラフGの辺eを縮約してできるグラフをG/e、辺eを除去してできるグラフをG\eと書く。
この記号を用いると、ネットワーク信頼度の展開公式は
Rel(G)=p・Rel(G/e)+(1-p)Rel(G\e)
ということになる。
この縮約と除去という操作に関して、グラフ理論では次のようなことが知られている。
(xとyを変数とする)多項式T(G)として、次の性質を満たす物を考える。
(ただし、ブリッジとは、その辺を取り除くと非連結になる辺のこと。ループとは、両端点が同じノードになっている辺のこと。)
- T(
 )=x, T(
)=x, T( )=y,
)=y,
- eがブリッジでもループでもない辺であるとき、
T(G) = T(G\e)+T(G/e),
- eがブリッジのとき、
T(G) = xT(G\e),
eがループのとき、
T(G) = yT(G\e).
これらの性質を満たす多項式は唯一つ存在することが知られており、
グラフのタット多項式と呼ばれている。
グラフのタット多項式はグラフのいろいろな性質を反映していることが知られていて、
その性質や拡張など、いろいろな面で研究されている。例えば、
- T(G)|x=1,y=1=「Gの全域木の個数」,
- T(G)|x=2,y=1=「Gの、サイクルを含まない部分グラフの個数」,
- T(G)|x=2,y=0=「Gの、有向サイクルを含まない向き付けの個数」
などが知られている。
(タット多項式はマトロイドの多項式に拡張され、マトロイドに関する多項式としてよく議論される。)
さて、ネットワーク信頼度の公式を眺めてみると、タット多項式とかなり似ている形をしていることに気づくだろう。実際、信頼度多項式はタット多項式を使って次のように書くことができる。
Rel(G) = pn-1(1ーp)m-(n+1)T(G)|x=1,y=1/(1-p)
<3章へ
|
目次
|
5章へ>

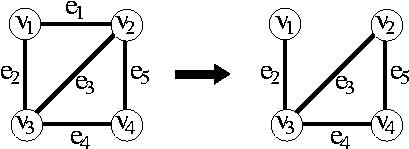

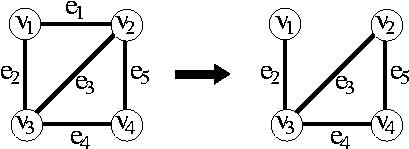
 )=x, T(
)=x, T( )=y,
)=y,