グラフGから(ある長さの)有向パスDPnへの準同型fがあるとする.
このとき,無向グラフから完全グラフへの準同型から彩色を作ったときのように,
Gの各頂点vに対して,fで写った先の頂点の番号で番号をつけてみる.
すると,このGの頂点の番号付けは,有向辺を向きに沿った方向に辿ると1増え,逆方向に辿ると1減ることが分かる.
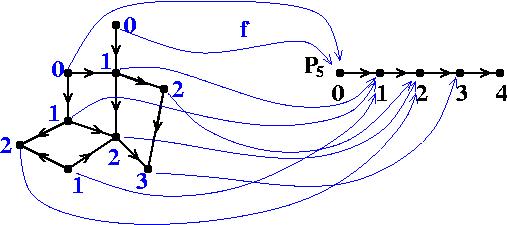
この番号付けを見ると,グラフGにおいて,どの(辺の向きを無視した)サイクルを見ても,順方向の向きの辺と逆方向の向きの辺の数はちょうど等しくなることが分かる. このようなグラフはbalanced graphと呼ばれる.
つまり,もしグラフGから(ある長さの)有向パスDPnへの順同型が存在すれば,Gはbalanced graphである,ということが分かったわけである.
それでは逆を考えてみよう. グラフGがbalanced graphであったとする.(Gは連結と仮定する.) このとき,ある頂点を適当に選んでその頂点に0を振り,そこから隣接する頂点に,辺が順方向に向き付けられていたら+1,逆方向だったら-1にしながら次々と番号を振っていくことにする. すると,この作業は途中で番号に矛盾が起きることなく終了する. (もし,ある頂点uから隣接する頂点vに振られた番号と,別の頂点からvに振られた番号が異なるとすると,順方向と逆方向の辺数が異なるサイクルが存在することになる.) すべての頂点に番号づけが与えられたら,一番小さい番号が0になるようにすべての頂点の番号を増やし,各頂点をDPnの同じ番号のついた頂点へ写す写像をfとすれば,このfがDPnへの準同型になることは簡単に確かめられる.
つまり,次の性質が示されたことになる.
|
性質: 有向グラフGから(ある長さの)有向パスへの準同型が存在することと, Gがbalanced graphであることは等価である. |