Homomorphisms of Graphs

クネーザーグラフへの準同型：グラフの分数彩色

前章では，K_nへの準同型がグラフのn-彩色と等価であることを見た．今度は別のグラフへの準同型を考えてみよう．

クネーザーグラフK_n:kとは，次のようなグラフである．

1～nの数字からk個を取り出した組をすべて考え，これらを頂点集合とする． (頂点数は全部で _nC_k個．)
2つの頂点に対して，それぞれのk個組の数字に共通の数字がなければ辺を結ぶ．

例えば，K_5:2は次の図のようになる．

さて，グラフGからこのクネーザーグラフK_n:kへの準同型について考えてみよう．

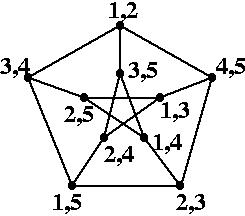
完全グラフK_nへの準同型を彩色に対応させたときと同じように，グラフGの各頂点vに，K_n:kへの準同型fの写す先の頂点のラベルをつけてみる．例えば下の例のようになる．

こうしてできたグラフGのラベル付けは，クネーザーグラフの定義とグラフの準同型の定義を合わせて考えれば，

各頂点にn色中k色を割り当て，
辺で隣接する2頂点は同じ色を共有しない，

ようなものになっているはずである．このような色の割当を，k重n-彩色(k-fold n-coloring)と呼ぶ．

逆に，グラフGにk重n-彩色が与えられれば，GからK_n:kへの準同型fを構成できるということも，(n-彩色の場合と同様)簡単に確認できる．つまり，次のようなことになっている．

性質：
グラフGからK_n:kへの準同型が存在することは，グラフGがk重n-彩色可能であることと等価である．

k重彩色という概念は，それ自身でも十分意味のある概念であるが，実は通常の彩色とも深い関連がある．

各kに対して，k重n-彩色可能であるような最小のnをχ_k(G)とする．このとき， lim_k→∞ χ_k(G)/kはある有理数χ_f(G)に収束することが知られており，これはグラフGの分数彩色数(fractional chromatic number)と呼ばれている． (詳しくは，例えば，E.R.Sheinerman & D.H.Ullman「Fractional Graph Theory」(John Wiley & Sons, 1997)などを参照するとよい．) 分数彩色数χ_f(G)は一般に通常の彩色数χ(G)以下になる(∵χ_k(G)は必ずkχ(G)以下になるから．)ことから，彩色数の下界値を与える一つの指標となる．

余談：グラフの分数彩色

少しadvancedな話になるが，彩色とk重彩色は次のように説明することもできる．
まず，彩色の方は次のように考えることができる．

まず，グラフの極大な独立集合，すなわち，頂点集合Vの部分集合でどの2頂点も辺で結ばれないものの中で極大なもの，のすべてを考える．(U₁, U₂, ..., U_tとする．)
これらで頂点集合を被覆することを考える．(つまり，V = ∪U_i となるようにU_iをいくつか選ぶ．)
それぞれの独立集合の部分集合はすべて独立集合になるので，上で作った被覆から，(極大ではないかもしれない)独立集合によるVの分割を得ることができる．
この分割で，U_iに入る頂点をiで塗ることにより，グラフの彩色ができる．
つまり，極大独立集合による頂点集合の被覆に必要な集合の数の最小値＝彩色数．

これを少しいじると，k重彩色の方は次のようになる．

同様に，グラフの極大な独立集合のすべてを考える．
今度は，極大独立集合で各頂点がk回ずつ被覆する(k重被覆という)ことを考える．(1つの極大独立集合を複数回使ってもよい．複数回使う場合は添字をt+i, 2t+i,...,のように，異なる番号に付け替える．)
各極大独立集合の部分集合をうまく選ぶことにより，各頂点がちょうどk回ずつ被覆されるようにできる．
各頂点vを，この被覆でvを覆っているk個のU_iの添字i達で塗ることにすると，これはk重彩色になる．
つまり，極大独立集合による頂点集合のk重被覆に必要な集合の数の最小値＝k重彩色数．

例えば下の例の場合，極大独立集合は
U₁={a,c,e,h}, U₂={a,c,f,h}, U₃={a,d,f,h}, U₄={b,d,g}, U₅={b,e,g}
の5個になっている．ここで，頂点を(1回ずつ)被覆する方法としては，例えば， U₁,U₂,U₄を使えばよい．(図の真中参照．) この被覆では頂点a,c,hのところでそれぞれU₁とU₂が重なっているので， U₂からa,c,hを除外すると，各頂点とも1回ずつの被覆(つまり，頂点集合の分割)になる．各U_iの添字で頂点に色を塗っていくと図の右端のように1, 2, 4の3色で彩色ができる．この例の場合，実際3つでの被覆が最小個数で，彩色数は3である．

一方，例えば，2重彩色を考えてみる．今度は，例えば，U₁,U₂,U₃,U₄,U₅の5個を使うと各頂点を2回ずつ被覆することができる．(下図真中参照．) ここで，a,hは3回ずつ被覆されているので，それぞれU₃から取り除いて2回ずつになるように調整しておき，ここから彩色を作ってみると，下図の右端のようになる．この場合，1,2,3,4,5の5色で2重彩色になっているので，2重5-彩色になる．実際，2重彩色数は5になる．さらに，分数彩色数はこの2重のときに既に達成されていて，χ_f(G)は5/2となっている．

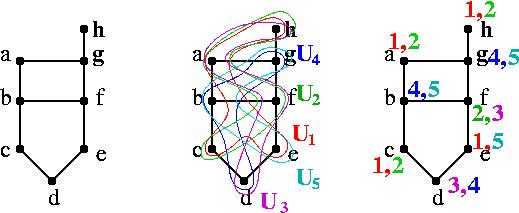
このように彩色とk重彩色を被覆の最小数として見直すと，次のように式で記述することができるようになる．まず，彩色数の方は，次のようになる．

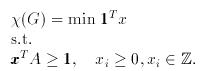
極大独立集合の隣接行列，つまり，列を頂点集合，行を極大独立集合の添字とし，各行を見た時にその独立集合に頂点が入っている部分が1，入ってない部分が0になるような行列をAとする．すると，彩色数は下の最適化問題の最適値に他ならない．

ただし，1はすべての要素が1のベクトル，xはi番目の要素がx_iのベクトルのことで，x_iは極大独立集合U_iを選んだら1，選ばなかったら0をとるような変数になっている．例えば上のグラフの例だと，次のように書き下される．

(注：この式の中ではx_iは0,1以外の正の整数をとってもよいことになっているが，実際には制約の不等式の左辺が1以上になるようにx_iを出来るだけ小さく選ぶ必要があるので，0か1しか選ばれない．)
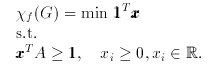
k重彩色の方は上の式で，不等式の左辺を要素がすべてkのベクトルに変えればよいだけである．
それでは，分数彩色数χ_fはどのようになるだろうか？これは自明なことではないのであるが，実は下の最適化問題の最適解がχ_fである．

(証明については，例えば，上の方でも触れているE.R.Sheinerman & D.H.Ullman「Fractional Graph Theory」(John Wiley & Sons, 1997)の1章などを見るとよい．) つまり，分数彩色数というのは，彩色数を定める最適化問題の定式化において，整数条件を緩和したもの，ということになっているのである．

<2章へ | 目次 | 4章へ>