という集合族が単体的複体であることを用い、その性質から上下限を与える話に触れた。
そして、7章では、このが単なる単体的複体ではなく、コーエン・マコーレーという性質を持つ単体的複体であることを用いることができることに触れた。
6章では、という集合族が単体的複体であることを用い、その性質から上下限を与える話に触れた。
そして、7章では、このが単なる単体的複体ではなく、コーエン・マコーレーという性質を持つ単体的複体であることを用いることができることに触れた。
それでは、このという集合族は、「コーエン・マコーレーな単体的複体」という以上の性質はないのだろうか？ もっと強い性質を持っていて、それを用いてもっとよい上下限を得ることはできないのだろうか？
それを考えるためには、という集合族が何なのか、
ということに答えないといけない。
定義に戻って考えてみると、は、あるグラフ(信頼度を計算しようとしているネットワーク)の辺の集合で、取り除いてもグラフを非連結にしないものの集合であった。
の極大な要素は、それ以上取り除くとグラフが非連結になる、という状況にある。
そのとき、取り除いた残りは、「全域木」という、サイクルを含まずすべてのノードを含むような部分グラフになっているはずである。
つまり、は、グラフの全域木の補集合(全域木の辺にならない辺の集合)およびその部分集合からなる集合族、ということができる。
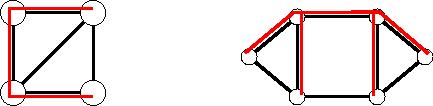
例えば、上の絵の赤で書いたものが全域木の例である。(他にもある。)
グラフにおいて、全域木とその部分集合からなる集合族は、 グラフィック・マトロイド(の独立集合族)と呼ばれている。 「マトロイド」というのは、線形代数を離散化したような抽象的な概念で、 離散数学における重要な、基本的な概念の一つである。 グラフィック・マトロイドというのは、グラフから生じるマトロイド、という意味である。
一方、上の、つまり、全域木の補集合とその部分集合からなる集合族は、コグラフィック・マトロイド(の独立集合族)と呼ばれている。
頭に「コ」がついているのは、グラフィック・マトロイドの「双対」である、ということである。
マトロイドが何であるのか、また、「双対」が何を意味するのかなどを説明するのには、またいろいろと多くの概念を紹介しないといけないので、別の機会に譲ることにする。 文献としては、
マトロイド(または、さらにコグラフィック・マトロイド)のf-列やh-列の特徴付けは完全には出来ておらず、数多くの予想が存在しているような状況のようである。 マトロイドの性質を深く研究し、その性質を明らかにしていくことから、いずれネットワーク信頼度の研究に寄与することになるかもしれない。
関連する問題など、前の章やそれ以外に関することがらも含め、以下のサーベイによく紹介されている。